MAKE A MEME
View Large Image
| View Original: | StationaryStatesAnimation.gif (300x280) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
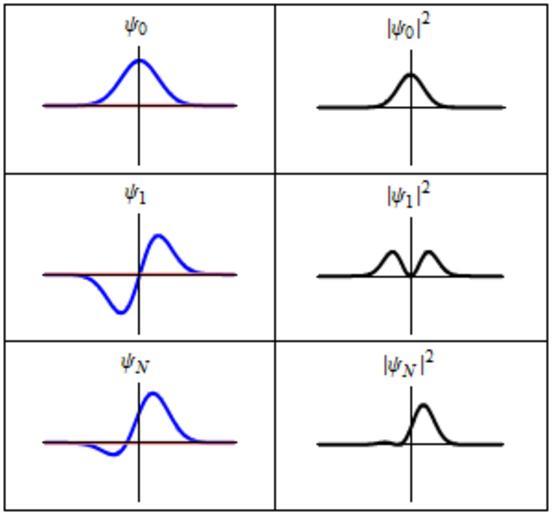
| Keywords: StationaryStatesAnimation.gif en Three wavefunction solutions to the Time-Dependent Schrödinger equation for a harmonic oscillator Left The real part blue and imaginary part red of the wavefunction Right The probability of finding the particle at a certain position The top two rows are the lowest two energy eigenstates and the bottom is the superposition state <math>\psi_N \psi_0+\psi_1 /\sqrt 2 </math> which is not an energy eigenstate The right column illustrates why energy eigenstates are also called stationary states Thus in every quantum stae there are certain preferred positions of maximum probability own Sbyrnes321 2011-03-20 <pre> Source code written in Mathematica 6 0 by Steve Byrnes Feb 2011 This source code is public domain Shows classical and quantum trajectory animations for a harmonic potential Assume m w hbar 1 ClearAll Global` Wavefunctions of the energy eigenstates psin_ x_ 2 n n -1/2 Pi -1/4 Exp-x 2/2 HermiteHn x; energyn_ n + 1/2; psitn_ x_ t_ psin x Exp-I energyn t; A non-stationary state SeedRandom1; psinonstationaryx_ t_ psit0 x t+psit1 x t /Sqrt2; Put all the plots together SetOptionsPlot PlotRange -> -1 1 Ticks -> None PlotStyle -> DirectiveThick Blue DirectiveThick Pink ; MakeFramet_ GraphicsGrid Plot Repsit0 x t Impsit0 x t x -5 5 PlotLabel -> Subscript\Psi 0 PlotAbspsit0 x t 2 x -5 5 PlotStyle -> DirectiveThick Black PlotLabel -> TraditionalFormAbsSubscript\Psi 0 2 Plot Repsit1 x t Impsit1 x t x -5 5 PlotLabel -> Subscript\Psi 1 PlotAbspsit1 x t 2 x -5 5 PlotStyle -> DirectiveThick Black PlotLabel -> TraditionalFormAbsSubscript\Psi 1 2 Plot Repsinonstationaryx t Impsinonstationaryx t x -5 5 PlotLabel -> Subscript\Psi N PlotAbspsinonstationaryx t 2 x -5 5 PlotStyle -> DirectiveThick Black PlotLabel -> TraditionalFormAbsSubscript\Psi N 2 Frame -> All ImageSize -> 300; output TableMakeFramet t 0 4 Pi 40/41 4 Pi/41 ; SetDirectory C \\Users\\Steve\\Desktop Export test gif output </pre> Cc-zero Images with Mathematica source code Animated GIF 1D quantum harmonic oscillators Animations of quantum wave functions 3x2 arrays Hermite functions | ||||