MAKE A MEME
View Large Image
| View Original: | QuantumHarmonicOscillatorAnimation.gif (300x373) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
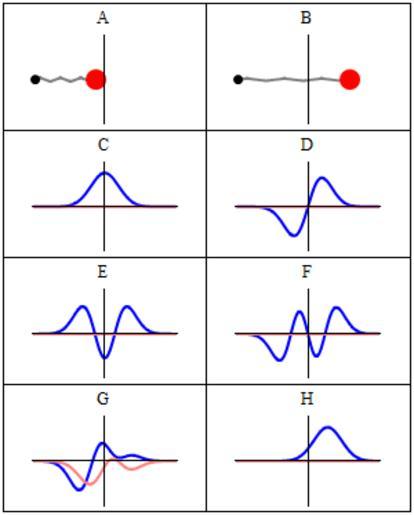
| Keywords: QuantumHarmonicOscillatorAnimation.gif en A harmonic oscillator in classical mechanics A-B and quantum mechanics C-H In A-B a ball attached to a spring gray line oscillates back and forth In C-H wavefunction solutions to the Time-Dependent Schrödinger Equation are shown for the same potential The horizontal axis is position the vertical axis is the real part blue or imaginary part red of the wavefunction C D E F are stationary states energy eigenstates which come from solutions to the Time-Independent Schrodinger Equation G-H are non-stationary states solutions to the Time-Dependent but not Time-Independent Schrödinger Equation G is a randomly-generated superposition of the four states E-F H is a coherent state Glauber state which somewhat resembles the classical state B own Sbyrnes321 2011-02-27 <pre> Source code written in Mathematica 6 0 by Steve Byrnes Feb 2011 This source code is public domain Shows classical and quantum trajectory animations for a harmonic potential Assume m w hbar 1 ClearAll Global` Wavefunctions of the energy eigenstates psin_ x_ 2 n n -1/2 Pi -1/4 Exp-x 2/2 HermiteHn x; energyn_ n + 1/2; psitn_ x_ t_ psin x Exp-I energyn t; A random time-dependent state SeedRandom1; CoefList TableRandom Exp2 Pi I Random n 0 4 ; CoefList CoefList/NormCoefList; Randpsix_ t_ SumCoefListn + 1 psitn x t n 0 4 ; A coherent state or Glauber state CoherentStateb_ x_ t_ Exp-Absb 2/2 Sumb n n -1/2 psitn x t n 0 15 ; Make the classical plots a red ball anchored to the origin by a gray spring classical1t_ max_ ListPlot max Cost 0 PlotStyle -> DirectiveRed AbsolutePointSize15; zigzagx_ Abs x + 0 25 - Roundx + 0 25 - 25; springx_ left_ right_ 9 zigzag3 x - left / right - left / 1 + Absright - left ; classical2t_ max_ Plotspringx -5 max Cost x -5 max Cost PlotStyle -> DirectiveGray Thick; classical3 ListPlot -5 0 PlotStyle -> DirectiveBlack AbsolutePointSize7; classicalt_ max_ label_ Showclassical2t max classical1t max classical3 PlotRange -> -5 5 -1 1 Ticks -> None Axes -> False True PlotLabel -> label AxesOrigin -> 0 0 ; Put all the plots together SetOptionsPlot PlotRange -> -1 1 Ticks -> None PlotStyle -> DirectiveThick Blue DirectiveThick Pink ; MakeFramet_ GraphicsGrid classicalt + 2 1 5 A classicalt 3 B Plot Repsit0 x t Impsit0 x t x -5 5 PlotLabel -> C Plot Repsit1 x t Impsit1 x t x -5 5 PlotLabel -> D Plot Repsit2 x t Impsit2 x t x -5 5 PlotLabel -> E Plot Repsit3 x t Impsit3 x t x -5 5 PlotLabel -> F Plot ReRandpsix t ImRandpsix t x -5 5 PlotLabel -> G Plot ReCoherentState1 x t ImCoherentState1 x t x -5 5 PlotLabel -> H Frame -> All ImageSize -> 300; output TableMakeFramet t 0 4 Pi 96/97 4 Pi/97 ; SetDirectory C \\Users\\Steve\\Desktop Export test gif output</pre> Cc-zero Animated GIF Images with Mathematica source code 1D quantum harmonic oscillators Animations of quantum wave functions Hermite functions | ||||