MAKE A MEME
View Large Image
| View Original: | Line integral of scalar field.gif (400x300) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
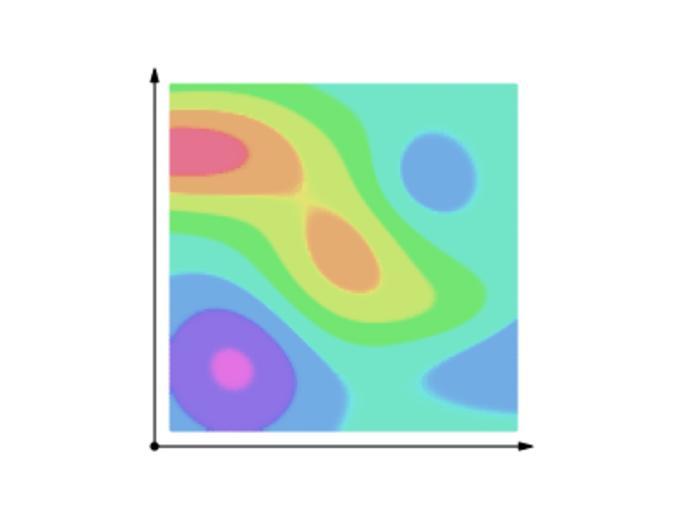
| Keywords: Line integral of scalar field.gif fa انتگرال خطی یک میدان اسکالر f مقدار انتگرال مساحت زیر منحنی C تعریف شده توسط سطح z f x y است intégrale curviligne d un champ scalaire f L aire sous la courbe C tracée sur la surface définie par z f x y est la valeur de l'intégrale it Integrale di linea di un campo scalare f Il valore dell'integrale è pari all'area sotto la curva C tracciata sulla superficie definita da z f x y ru Иллюст ация к иволинейного интег ала пе вого ода на скаля ном поле own 2012-07-24 Lucas V Barbosa Video version higher resolution longer pauses Line integral of a vector field Static version of this abstract scalar field with scale Assessment Assessments 1 2012 1 1 f Line integral of scalar field English A scalar field has a value associated to each point in space Examples of scalar fields are height temperature or pressure maps In a two-dimensional field the value at each point can be thought of as a height of a surface embedded in three dimensions The line integral of a curve along this scalar field is equivalent to the area under a curve traced over the surface defined by the field In this animation all these processes are represented step-by-step directly linking the concept of the line integral over a scalar field to the representation of integrals familiar to students as the area under a simpler curve A breakdown of the steps The color-coded scalar field f and a curve C are shown The curve C starts at a and ends at b The field is rotated in 3D to illustrate how the scalar field describes a surface The curve C in blue is now shown along this surface This shows how at each point in the curve a scalar value the height can be associated The curve is projected onto the plane XY in gray giving us the red curve which is exactly the curve C as seen from above in the beginning This is red curve is the curve in which the line integral is performed The distances from the projected curve red to the curve along the surface blue describes a curtain surface in blue The graph is rotated to face the curve from a better angle The projected curve is rectified made straight and the same transformation follows on the blue curve along the surface This shows how the line integral is applied to the arc length of the given curve The graph is rotated so we view the blue surface defined by both curves face on This final view illustrates the line integral as the familiar integral of a function whose value is the signed area between the X axis the red curve now a straight line and the blue curve which gives the value of the scalar field at each point Thus we conclude that the two integrals are the same illustrating the concept of a line integral on a scalar field in an intuitive way Animations of calculus Mathematical animations Line integral Scalar fields Featured animations | ||||
