MAKE A MEME
View Large Image
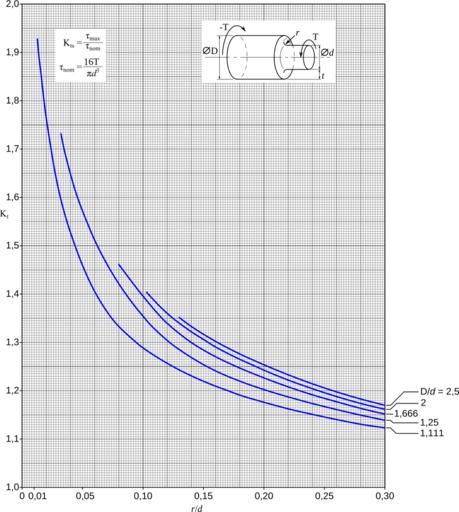
| View Original: | Kt arbre epaule torsion.svg (672x750) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
| Keywords: Kt arbre epaule torsion.svg fr Abaque de facteurs de concentration de contrainte K<sub>t</sub> dans le cas d'un arbre Ă©paulĂ© en torsion en Stress concentration factors K<sub>t</sub> chart for a shaft with shoulder fillet in torsion 2013-04-24 11 31 46 own from Pilkey Walter D Peterson's Stress Concentration Factors 2<sup>nd</sup> ed Wiley sons 1997 ISBN 97-0-471-53849-3 p 166 Cdang inkscape cdang ; Calculation <math>\mathrm K_t \mathrm C _1 + \mathrm C _2 \alpha + \mathrm C _3 \alpha 2 + \mathrm C _4 \alpha 3</math> <math>\alpha \frac 2t \mathrm D </math> t is the fillet height t D - d /2 wikitable + Coefficient for the calculation of K<sub>t</sub> - β t/r scope col 0 25 ‰¤ β ‰¤ 4 0 - scope row C<sub>1</sub> <math>0 905 + 0 783 \sqrt \beta - 0 075 \beta</math> - scope row C<sub>2</sub> <math>-0 437 - 1 969 \sqrt \beta + 0 553 \beta</math> - scope row C<sub>3</sub> <math>1 557 + 1 073 \sqrt \beta - 0 578 \beta</math> - scope row C<sub>4</sub> <math>-1 061 + 0 171 \sqrt \beta - 0 086 \beta</math> scilab source <source lang scilab >// // Initialisation // clear; clc; // // Fonctions // // Saisie des paramètres gĂ©omĂ©triques function A param_geo A 1 input grand diamètre D ; A 2 input petit diamètre d ; A 3 input rayon r ; endfunction // Calcul en torsion function Kt Kt_torsion Alpha Beta coefs 0 905 0 783 -0 075; -0 437 -1 969 0 553; 1 557 1 073 -0 578; -1 061 0 171 0 086; C coefs 1 + coefs 2 sqrt Beta + coefs 3 Beta; polynome poly C' x c ; Kt horner polynome Alpha ; endfunction // // Programme principal // // Accueil disp Facteurs de concentration de contrainte dun arbre Ă©paulĂ© disp W D Pilkey Petersons Stress Concentration factors Wiley sons 1997 // A 1 D ; A 2 d ; A 3 r A param_geo ; t 0 5 A 1 - A 2 ; // hauteur de filet Beta t/A 3 ; // t/r Alpha 2 t/A 1 ; Kt_to Kt_torsion Alpha Beta ; if Beta < 0 25 Beta > 4 then disp Torsion attention valeur extrapolĂ©e ; end disp 'Kt torsion '+string Kt_to ; </source> cc-zero Uploaded with UploadWizard Stress concentration Torsion | ||||