MAKE A MEME
View Large Image
| View Original: | Höger eller vänster.gif (384x384) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
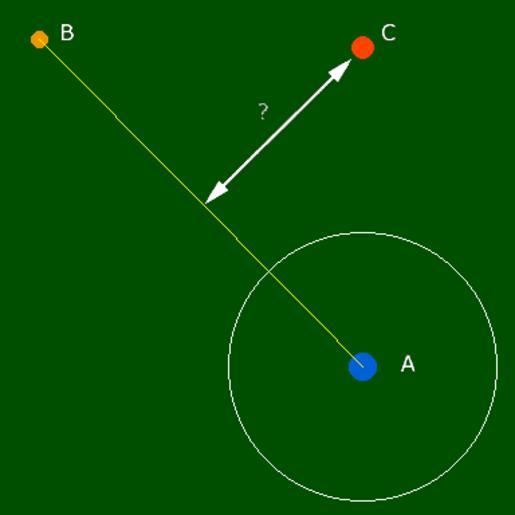
| Keywords: Höger eller vänster.gif Ett exempel på vektorgeometri beskrivning nedan User Solkoll on http //sv wikipedia org sv wikipedia Solkoll rum Bildbeskrivning Lilla blåa sv Anna <math>A</math> står på en sv gräsmatta sv komplexa talplanet och tittar på den oranga sv bollen <math>B</math> Den rödspräckliga sv Katten Catta <math>C</math> ligger och latar sig i solen scenen sedd från ovan Nu är frågan ligger Catta till höger eller till vänster om lilla Annas siktlinje Ett sätt att ta reda på det är att translatera förflytta hela bilden ovan så att lilla Anna hamnar mitt i bilden och sedan rotera scenen på ett sådan sätt så att bollen befinner sig på den positiva x-axeln Anna tittar rakt åt höger Därefter kan man se om Catta befinner sig ovan eller nedanför x-axeln om C parameterns sv imaginärdel är positiv eller negativ För att beräkna detta börjar vi först med att skapa två nya sv vektorer Punkt <math>P</math> och Rotation <math>R</math> ur de tre vi redan har <math>A B C </math> Den nya parametern <math>P</math> är längden och vinkeln från <math>A</math> till <math>C</math> och motsvarar alltså av vektorn mellan lilla Anna och Catta ej markerad i bilden Den vektorn skapas genom att dra ifrån subtrahera lilla Annas position från Cattas Vi gör även likadant med bollen <math>P C - A</math> <math>R B - A</math> 0 cellpadding 4 E7E7E7 Vad vi gör här är att förflytta talplanet på ett sådant sätt så att lilla Anna kommer att befinna sig i sv origo <math>P</math> och <math>R</math> är Cattas och bollens nya positioner i förhållande till detta Lilla Annas nya position behvöer vi inte beräkna då den motsvarar <math>origo A - A 0</math> och det vet vi ju redan Vad <math>R</math> beträffar så är vi endast intresserade av dess vinkel siktlinjens vinkel i förhållande till sv x-axeln och inte av dess längd Därför delar vi <math>R</math> med sitt eget sv absolutbelopp <math>R R / R </math> 0 cellpadding 4 E7E7E7 Det här metoden kallas för att beräkna en normalvektor eller vektorns normal En sådan har alltid längden 1 0 och används för att ange en riktning Nyttan med en sådan är att man kan använda den för att lägga till normalens vinkeln till en annan vektors vinkel Det görs med hjälp av en vektormultiplikation Nu kommer <math>R</math> att ha längden absolutbeloppet 1 0 och peka på skärningspunkten mellan sv enhetscirkeln runt lilla Anna i bilden och siktlinjen Den punkten motsvara sv cosinus och sv sinus för sv vinkeln mellan siktlinjen och x-axeln Vi behöver vinkeln för att veta hur långt vi skall rotera tillbaka scenen för att bollen skall hamna på den positiva x-axeln Men för att kunna göra detta så måste vi rotera medurs lika långt som vinkeln pekar moturs Vi måste alltså skapa en medursvinkel av motursvinkeln spegla den över x-axeln Det görs genom att beräkna dess sv komplexkonjugat <math>R \bar R </math> Nu behöver vi inte ge oss på att rotera hela scenen utan det är endast imaginärdelen hos den roterade parametern <math>P</math> som vi behöver ta reda på Eftersom det inte är ett komplext tal så behöver vi heller inte använda komplexa tal för att beräkna den Därför bryter vi ur real och imaginärdelarna ur <math>P</math> och <math>R</math> Dom kallar vi <math>Px</math> och <math>Py</math> samt <math>Rx</math> och <math>Ry</math> Sedan beräknas resultatet <math>resultat Rx Py + Ry Px</math> Om nu <math>resultat < 0</math> så befinner sig Catta till höger om lilla Annas siktlinje och om <math>resultat > 0</math> så är Catta till vänster Skulle till äventyrs <math>resultat 0</math> så befinner sig Catta mitt på siktlinjen Triangelns area Om vi nu tänker oss en sv triangeln som bildas av dom tre sv punkterna i bilden ovan <math>A -> B -> C -> A</math> så kan man ju alltid undra hur stor dess sv area är Nu råkar det falla sig så att vi i pricip har allt vi behöver för att beräkna den vad vi skulle ha gjort var att spara värdet på parametern <math>R</math> innan vi delade den med sitt eget absolutbelopp tidigare Vi beräknar den på nytt <math>R B - A</math> Nu är det bara längden på <math>R</math> vi är intresserade av avståndet mellan <math>A</math> och <math>B</math> det motsvarar triangelns baslinje Nästa steg blir att beräkna längden på den och sparar beloppet i <math>b</math> <math>b R </math> Sådär nu har vi triangelns sv bas men hur stor är dess sv höjd Det har vi redan tagit reda på när vi testade för höger/vänster ovan Det vi beräknade är egentligen avståndet till linjen så därför motsvarar absolutbeloppet av <math>resultat</math> triangelns höjd vi beräknar även den <math>h resultat </math> Sådär nu är det bara att sätta in dessa i den sedvanliga sv formeln som brukas för att beräkna en triangels area <math>arean bh/2</math> Se även sv Bild Triangel ytan GIF page is was here 6 december 2004 kl 00 40 Solkoll 384x384 2 314 bytes <span class comment > kommer Solkoll sv Kategori Vektorgeometri </span> Uploaded using http //tools wikimedia de/~magnus/commonshelper php CommonsHelper or http //tools wikimedia de/~magnus/pushforcommons php PushForCommons Check categories 2009 November 16 sv wikipedia Linjärt_rum 3 Linear algebra Files by User Solkoll from sv wikipedia Abstract algebra | ||||