MAKE A MEME
View Large Image
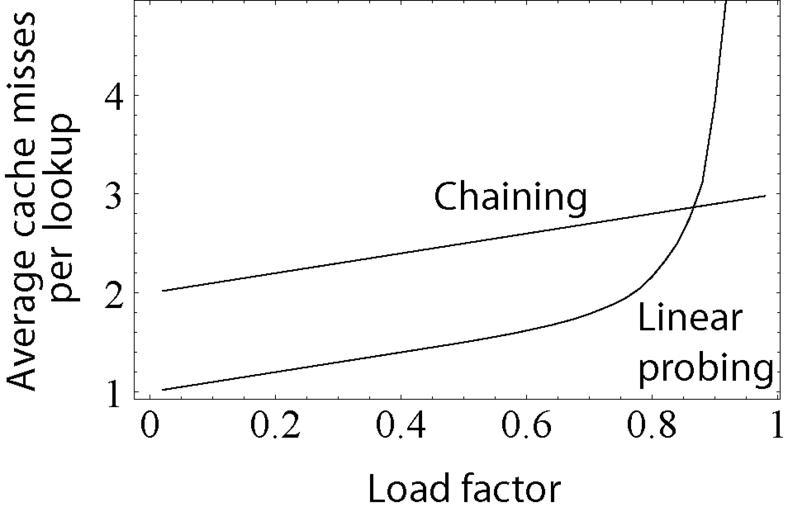
| View Original: | Hash table average insertion time.png (954x620) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
| Keywords: Hash table average insertion time.png graph Shows the average number of cache misses expected when inserting into a hash table with various collision resolution mechanisms; on modern machines this is a good estimate of actual clock time required This seems to confirm the common heuristic that performance begins to degrade at about 80 table density Created in Mathematica Illustrator and Photoshop It is based on a simulated model of a hash table where the hash function chooses indexes for each insertion uniformly at random The parameters of the model were A table size of 1 000 elements An L1 cache line size of 16 words as on the Pentium 4 L2 cache effects are not accounted for You may be curious what happens in the case where no cache exists In other words how does the number of probes number of reads number of comparisons rise as the table fills The curve is similar in shape to the one above but shifted left it requires an average of 24 probes for an 80 full table and you have to go down to a 50 full table for only 3 probes to be required on average This suggests that in the absence of a cache ideally your hash table should be about twice as large for probing as for chaining Author's Own Work Derrick Coetzee User Dcoetzee Mathematica Coding Because the linear probing values varied widely according to the random choices used to fill the table I took the average value over 25 runs The rather inefficient Mathematica code used to generate the table follows <pre> <<Statistics`DescriptiveStatistics`; ftablesize_ points_ cachewords_ Module i r j compares1 compares2 k slots1 slots2 slots1 Table0 i 1 tablesize ; slots2 Table0 i 1 tablesize ; Table Fori 0 i<FloorLengthslots1/ points+1 i++ r RandomInteger 1 Lengthslots1 ; slots1r++; Fori 0 i<Lengthslots1/ points+1 i++ r RandomInteger 1 Lengthslots2 ; Forj r slots2j>0 j Ifj\EqualLengthslots2 1 j+1; slots2j++; compares2 0; Fori 1 i< Lengthslots2 i++ Forj i slots2j>0 j Ifj\EqualLengthslots2 1 j+1; compares2+ CeilingIfj\GreaterEquali j-i j+Lengthslots2-i/cachewords; NApplyPlus slots1/Lengthslots1+2 Ncompares2/Lengthslots2+1 k 1 points ; t Tablef1000 49 16 i 1 25 ; Export Hash_table_average_insertion_time eps ShowMapListPlot PlotJoined\RuleTrue Frame\RuleTrue FormatType\RuleTraditionalForm FrameLabel\Rule Density of table Average cache misses per insertion Axes\RuleFalse Table i/50 MeanTabletk i j k 1 Lengtht j 1 2 i 1 Lengtht1 </pre> Hash tables Images with Mathematica source code | ||||