MAKE A MEME
View Large Image
| View Original: | Discrete Hilbert transforms of a cosine function, using piecewise convolution.jpg (1108x576) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
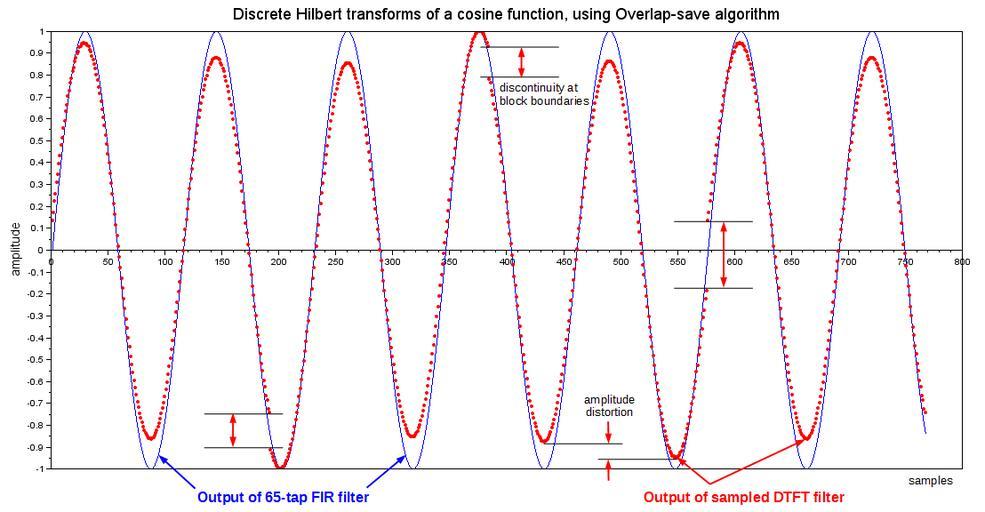
| Keywords: Discrete Hilbert transforms of a cosine function, using piecewise convolution.jpg en The blue graph shows a sine function that was created by computing the Discrete Hilbert transform of a cosine function The cosine function was divided into 4 overlapping segments which were individually convolved with an FIR Hilbert transform filter and the 4 output segments were seamlessly pieced together If the DFT of the FIR filter is replaced by the trivial samples of the DTFT of an IIR Hilbert transform filter the cosine function segments are effectively convolved with a periodic summation of the IIR filter That results in some frequency-dependent amplitude distortion and discontinuities at the segment boundaries Examples of these effects are shown in the red graph 2015-03-21 own Bob K other versions Scilab script <source lang Scilab > // Create a 64th-order Hilbert transform filter M 65; h hilb M ; // applies a rectangular window to the IIR function // Derive overlap-save parameters overlap M-1; N 4 overlap; // an efficient block-size step_size N-overlap; M2 overlap/2; // length of the edge effects for a zero-phase non-causal filter h h 1+M2 M zeros 1 N-M h 1 M2 ; // convert filter to zero-phase H1 fft h -1 ; // transfer function H2 i 0 -ones 1 N/2-1 ones 1 N/2 ; // or just sample the DTFT // Create an input function num_steps 4; // signal length in steps n 0 num_steps step_size+overlap -M2; // sample indices minus filter delay cycles_per_step 5/3; // just a non-integer cycles_per_sample cycles_per_step / step_size; x cos 2 pi cycles_per_sample n ; // transform a pure sinusoid // Overlap-Save convolution position 0; while position+N < length x yt real fft fft x position+ 1 N -1 H1 1 ; y1 position+ 1 step_size yt 1+M2 N-M2 ; // The next 2 lines are equivalent so the 2nd one is commented out yt real fft fft x position+ 1 N -1 H2 1 ; // yt imag hilbert x position+ 1 N ; y2 position+ 1 step_size yt 1+M2 N-M2 ; position position + step_size; end // Compare the results y1 y1 / max abs y1 ; y2 y2 / max abs y2 ; plot y1 'b' ; plot y2 'r ' ; title Discrete Hilbert transforms of a cosine function using Overlap-save algorithm fontsize 4 ; ylabel amplitude fontsize 3 ; a gca ; a x_location origin ; a children 1 children mark_size 4; // size of red dots </source> cc-zero Uploaded with UploadWizard Signal processing | ||||