MAKE A MEME
View Large Image
| View Original: | DiffusionMicroMacro.gif (360x300) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
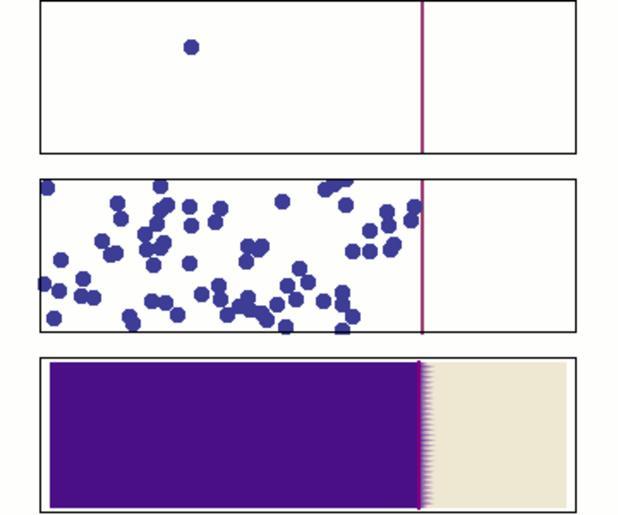
| Keywords: DiffusionMicroMacro.gif en Diffusion from a microscopic and macroscopic point of view Initially there are solute molecules on the left side of a barrier purple line and none on the right The barrier is removed and the solute diffuses to fill the whole container Top A single molecule moves around randomly Middle With more molecules there is a clear trend where the solute fills the container more and more evenly Bottom With an enormous number of solute molecules the randomness is gone The solute appears to move smoothly and systematically from high-concentration areas to low-concentration areas following Fick's laws Image is made in Mathematica source code below own Sbyrnes321 2010-01-16 Diffusion Animations of physics Images with Mathematica source code Animated GIF << Mathematica source code >> <pre> Source code written in Mathematica 6 0 by Steve Byrnes 2010 I release this code into the public domain Sorry it's messy email me any questions Particle simulation SeedRandom1; NumParticles 70; xMax 0 7; yMax 0 2; xStartMax 0 5; StepDist 0 04; InitParticleCoordinates Table RandomReal 0 xStartMax RandomReal 0 yMax i 1 NumParticles ; StayInBoxXx_ Ifx < 0 -x Ifx > xMax 2 xMax - x x; StayInBoxYy_ Ify < 0 -y Ify > yMax 2 yMax - y y; StayInBoxXYxy_ StayInBoxXxy1 StayInBoxYxy2 ; StayInBarXx_ Ifx < 0 -x Ifx > xStartMax 2 xStartMax - x x; StayInBarYy_ Ify < 0 -y Ify > yMax 2 yMax - y y; StayInBarXYxy_ StayInBarXxy1 StayInBarYxy2 ; MoveAStepxy_ StayInBoxXYxy + RandomReal -StepDist StepDist RandomReal -StepDist StepDist ; MoveAStepBarxy_ StayInBarXYxy + RandomReal -StepDist StepDist RandomReal -StepDist StepDist ; NextParticleCoordinatesParticleCoords_ MoveAStep / ParticleCoords; NextParticleCoordinatesBarParticleCoords_ MoveAStepBar / ParticleCoords; NumFramesBarrier 10; NumFramesNoBarrier 50; NumFrames NumFramesBarrier + NumFramesNoBarrier; ParticleCoordinatesTable Table0 i 1 NumFrames ; ParticleCoordinatesTable1 InitParticleCoordinates; Fori 2 i < NumFrames i++ Ifi < NumFramesBarrier ParticleCoordinatesTablei NextParticleCoordinatesBarParticleCoordinatesTablei - 1 ParticleCoordinatesTablei NextParticleCoordinatesParticleCoordinatesTablei - 1;; Plot full particle simulation makeplotbarParticleCoord_ ListPlot ParticleCoord xStartMax 0 xStartMax yMax Frame -> True Axes -> False PlotRange -> 0 xMax 0 yMax Joined -> False True PlotStyle -> PointSize 03 Thick AspectRatio -> yMax/xMax FrameTicks -> None; makeplotParticleCoord_ ListPlotParticleCoord Frame -> True Axes -> False PlotRange -> 0 xMax 0 yMax Joined -> False PlotStyle -> PointSize 03 AspectRatio -> yMax/xMax FrameTicks -> None ParticlesPlots JoinTablemakeplotbarParticleCoordinatesTablei i 1 NumFramesBarrier TablemakeplotParticleCoordinatesTablei i NumFramesBarrier + 1 NumFrames ; Plot just the first particle in the list Actually the fifth particle looks better FirstParticleTable 5 / ParticleCoordinatesTable; FirstParticlePlots JoinTablemakeplotbarFirstParticleTablei i 1 NumFramesBarrier TablemakeplotFirstParticleTablei i NumFramesBarrier + 1 NumFrames ; Continuum solution I can use the simple diffusion-on-an-infinite-line formula as long as I correctly periodically replicate the initial condition Actually just computed nearest five replicas in each direction that was a fine approximation k diffusion coefficient visually matched to simulation k 0007; ux_ t_ Ift 0 Ifx < xStartMax 1 0 1/2 Sum Erf x - -xStartMax + 2 n xMax /Sqrt4 k t - Erf x - xStartMax + 2 n xMax /Sqrt4 k t n -5 5 ; ContinuumPlots Join TableShow DensityPlot1 - ux 0 x 0 xMax y 0 yMax ColorFunctionScaling -> False AspectRatio -> yMax/xMax FrameTicks -> None ListPlot xStartMax 0 xStartMax yMax Joined -> True PlotStyle -> Thick Purple i 1 NumFramesBarrier Table DensityPlot1 - ux tt x 0 xMax y 0 yMax ColorFunctionScaling -> False AspectRatio -> yMax/xMax FrameTicks -> None tt 1 NumFramesNoBarrier ; Combine and export TogetherPlots TableGraphicsGrid FirstParticlePlotsi ParticlesPlotsi ContinuumPlotsi Spacings -> Scaled0 2 i 1 NumFrames ; Export test gif JoinTogetherPlots TableGraphics i 1 5 DisplayDurations -> 10 AnimationRepititions -> Infinity </pre> | ||||